Custom Grid Components

We can make our own “custom grid components” using Python 3 Script components. This page contains some (hopefully) interesting exercises in making customized grids.

Note

You can get a completed Grasshopper document containing implementations for everything on this page here.

Parallelogram Grids

We can make our own parallelogram grids, extending the Rectangular component to slanted grids. Of course, this could be done by shearing the cells or points created by the Rectangular component, but using a Python 3 Script component is a pretty easy way to make this work.

Inputs

• size_u, type-hinted as float

• size_v, type-hinted as float

• extent_u, type-hinted as int

• extent_v, type-hinted as int

• theta, type-hinted as float

Outputs

• cells, type-hinted as Polyline

• points, type-hinted as Point3d

Source Code

from math import cos, sin, radians

import ghpythonlib.treehelpers as th
import rhinoscriptsyntax as rs
from Rhino.Geometry import Vector3d

theta = radians(theta)

u_basis = size_u * Vector3d(1, 0, 0)
v_basis = size_v * Vector3d(cos(theta), sin(theta), 0)

# Generate points
points = []
for u in range(extent_u + 1):
    row = []
    for v in range(extent_v + 1):
        row.append(u * u_basis + v * v_basis)
    points.append(row)

# Generate cells
cells = []
for u in range(extent_u):
    row = []
    for v in range(extent_v):
        row.append(rs.AddPolyline(
            [
                points[u][v],
                points[u + 1][v],
                points[u + 1][v + 1],
                points[u][v + 1],
                points[u][v]  # repeat the first point to make a closed loop
            ]
        ))
    cells.append(row)

points = th.list_to_tree(points)
cells = th.list_to_tree(cells)

Generic Hexagonal

We can generalize the Hexagonal component to vary the lengths of the 3 pairs of parallel sides on each hexagon. For this type of grid, we don’t care as much about the corner points of the grid because, as in Hexagonal, attempting to index the grid points isn’t as straightforward as it is with a rectilinear grid.

To create this type of grid, it’s easier to use a basis with more than 2 vectors in order to find the corners of the cells, then use the corners of the cells to compute their centroids.

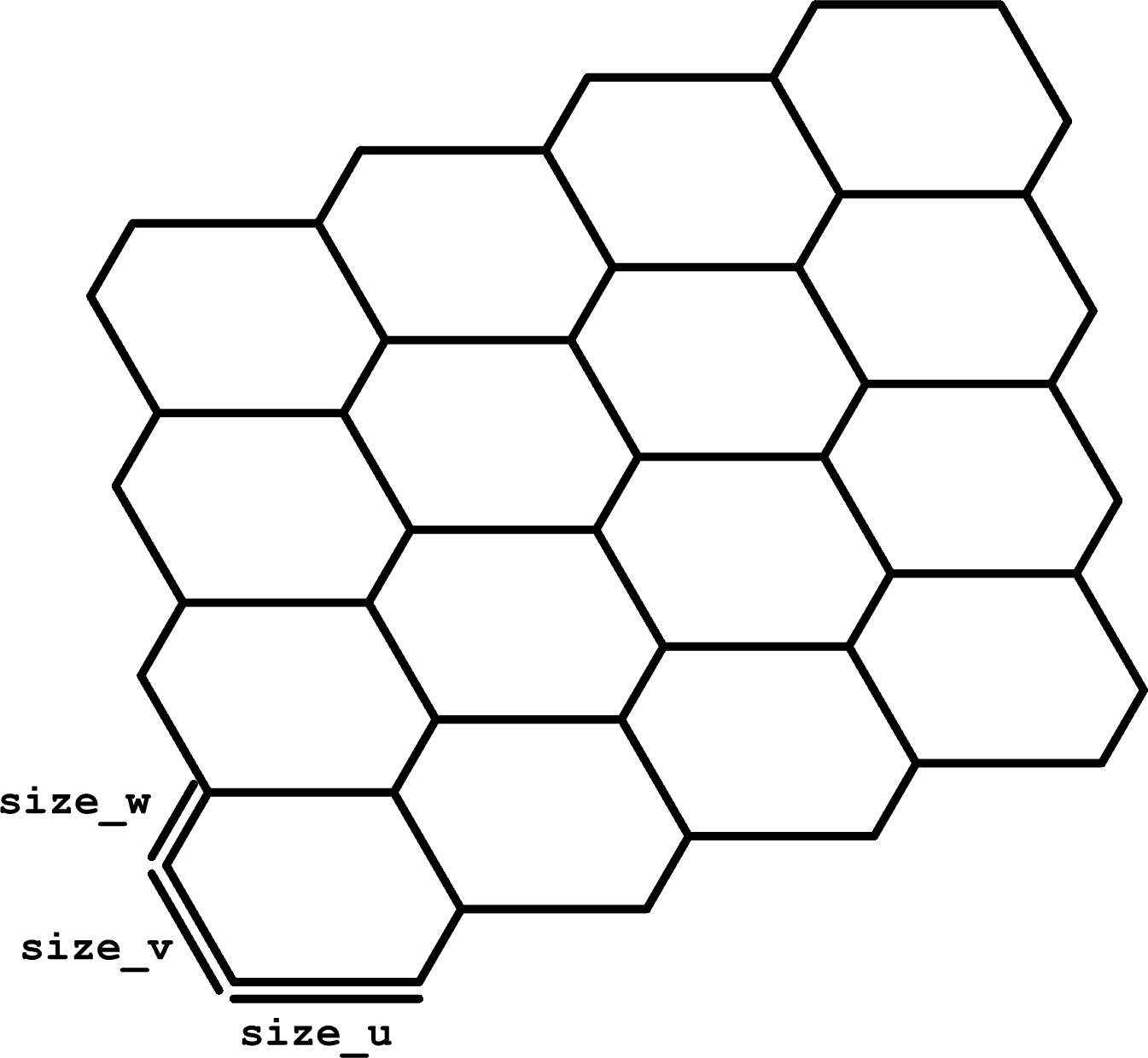
Inputs

• size_u, type-hinted as float

• size_v, type-hinted as float

• size_w, type-hinted as float

• extent_u, type-hinted as int

• extent_v, type-hinted as int

• extent_w, type-hinted as int

Outputs

• cells, type-hinted as Polyline

• points, type-hinted as Point3d

Source Code

from math import cos, sin, pi

import ghpythonlib.treehelpers as th
import rhinoscriptsyntax as rs
from Rhino.Geometry import Vector3d

u_basis = size_u * Vector3d(1, 0, 0)
v_basis = size_v * Vector3d(cos(-pi / 3), sin(-pi / 3), 0)
w_basis = size_w * Vector3d(cos(pi / 3), sin(pi / 3), 0)

# Generate cells and points in tandem
cells = []
points = []
for i in range(extent_right):
    cell_row = []
    point_row = []
    for j in range(extent_up):
        west_corner = i * (u_basis + w_basis) + j * (w_basis - v_basis)
        corners = [
            west_corner,
            west_corner + v_basis,
            west_corner + v_basis + u_basis,
            west_corner + v_basis + u_basis + w_basis,
            west_corner + u_basis + w_basis,
            west_corner + w_basis,
            west_corner
        ]
        cell_row.append(rs.AddPolyline(corners))
        point_row.append(sum(corners[:-1], start=Vector3d(0, 0, 0)) / 6)
    cells.append(cell_row)
    points.append(point_row)

cells = th.list_to_tree(cells)
points = th.list_to_tree(points)

Generic Regular Monotilings

In general, you can use a strategy similar to the one we used for the hexagonal grid to generate any regular tiling using a monotile. We need to be able to identify the vectors used in the construction of the monotile.

The monotile of choice.

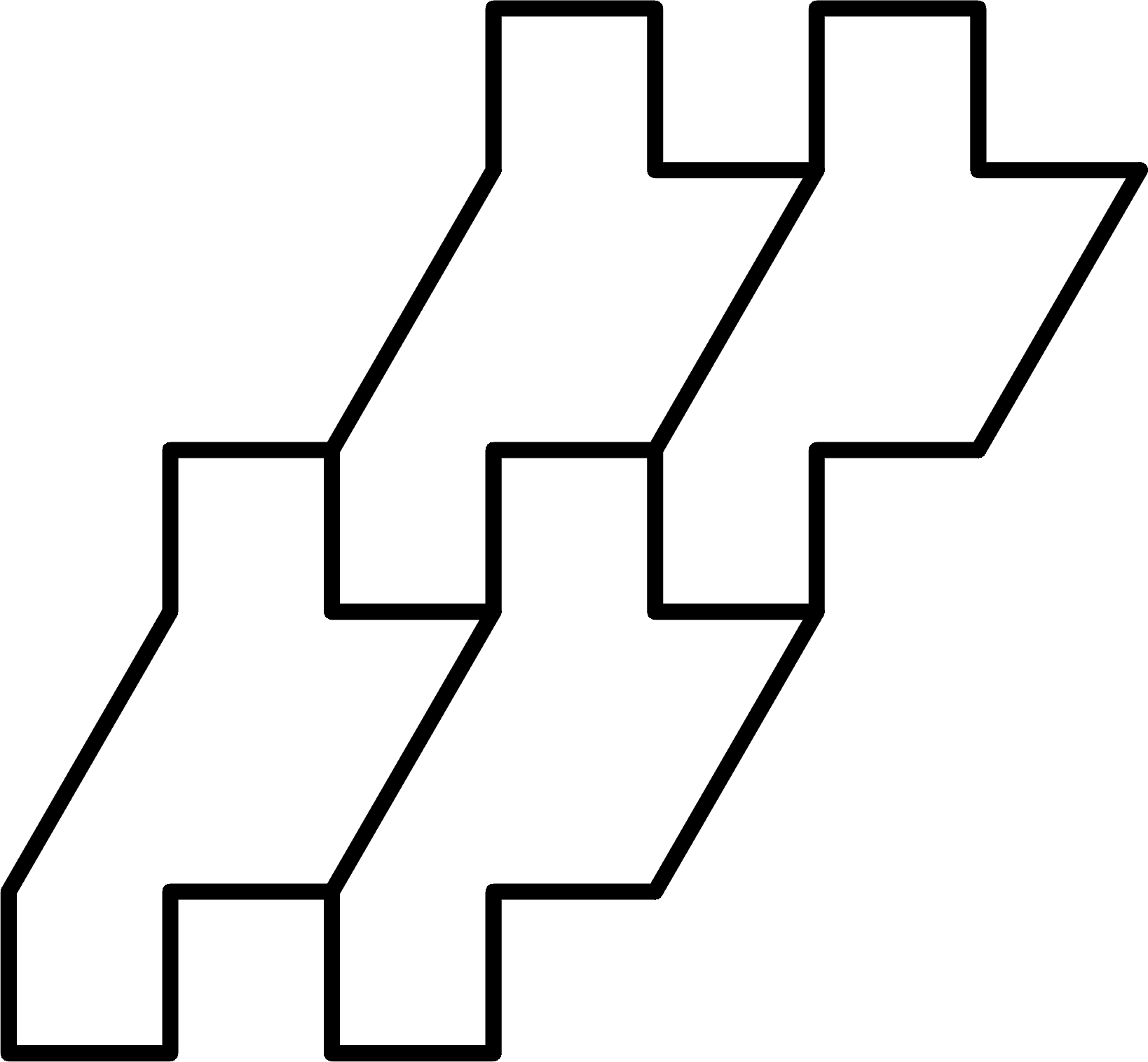
How this monotile tiles.

The monotile of choice.

How this monotile tiles.

We can choose a start point on the monotile, create the remaining points by adding these vectors, and identify which point makes the start point on a neighbor tile. Starting at the bottom of the left slanted line, this monotile can be created by chaining together the following vectors:

\[\begin{split}\begin{flalign} &\begin{bmatrix} 0 & \frac{-1}{2} \end{bmatrix}\\ &\begin{bmatrix} \frac{1}{2} & 0 \end{bmatrix}\\ &\begin{bmatrix} 0 & \frac{1}{2} \end{bmatrix}\\ &\begin{bmatrix} \frac{1}{2} & 0 \end{bmatrix}\\ &\begin{bmatrix} \frac{\sqrt{3}}{2} & \frac{1}{2} \end{bmatrix}\\ &\begin{bmatrix} \frac{-1}{2} & 0 \end{bmatrix}\\ &\begin{bmatrix} 0 & \frac{1}{2} \end{bmatrix}\\ &\begin{bmatrix} \frac{-1}{2} & 0 \end{bmatrix}\\ &\begin{bmatrix} 0 & \frac{-1}{2} \end{bmatrix}\\ &\begin{bmatrix} \frac{-\sqrt{3}}{2} & \frac{-1}{2} \end{bmatrix}\\ \end{flalign}\end{split}\]

Computing the Vectors for Any Monotile

I specifically chose these vectors to make an interesting shape and tiling, but you could start with a regularly tiling monotile and calculate the vectors needed after the fact, too.

To do this, create a Python 3 Script component with an input called monotile, type-hinted as Polyline. Pipe a Curve input set to your monotile polyline to monotile. Place points at the start point of your monotile and the location of the next tile to the right and the next tile up from the initial monotile (see the example image). Set 3 point inputs to these points and pipe them to Point3d inputs called start, right_start, and up_start, respectively. Make an output called path, type-hinted to Vector3d, and two called right_index and up_index, type-hinted to int.

Pasting the following code into the script block, path should be a list of vectors suitable to construct your monotile. right_index and up_index will be set to the indices of the points in the path where the tile to the right and up will start.

from Rhino.Geometry import Polyline, Point3d, Vector3d

start_index: int = monotile.FindIndex(lambda x: start.EpsilonEquals(x, 1e-6))
right_index: int = monotile.FindIndex(lambda x: right_start.EpsilonEquals(x, 1e-6))
up_index: int = monotile.FindIndex(lambda x: up_start.EpsilonEquals(x, 1e-6))

points = list(monotile)
points = points[start_index:] + points[:start_index]
right_index -= start_index
if right_index < 0:
    right_index += len(points)
up_index -= start_index
if up_index < 0:
    up_index += len(points)

path = []
for i in range(1, len(points)):
    path.append(points[i] - points[i - 1])
path.append(points[-1] - points[0])

Assuming you have a path of vectors corresponding to each step in the path and the indices corresponding to the steps in the path where the tiles to the right and above start, you can create a new Python 3 Script with the following setup:

Inputs

• extent_right, type-hinted as int

• extent_up, type-hinted as int

• path, type-hinted as Vector3d, set to List Access

• right_index, type-hinted as int

• up_index, type-hinted as int

path, right_index, and up_index be piped directly from the outputs of the path calculation script component. Alternatively, you can enter them directly in panels.

Outputs

• cells, type-hinted as Polyline

Source Code

import ghpythonlib.treehelpers as th
import rhinoscriptsyntax as rs
from Rhino.Geometry import Vector3d

cumulative_vectors = [Vector3d(0, 0, 0)]
for i, step in enumerate(path):
    cumulative_vectors.append(cumulative_vectors[i] + step)

basis_right = cumulative_vectors[right_index]
basis_up = cumulative_vectors[up_index]

cells = []
for i in range(extent_right):
    row = []
    for j in range(extent_up):
        start_point = i * basis_right + j * basis_up
        points = [
            start_point + vector
            for vector in cumulative_vectors
        ]
        row.append(rs.AddPolyline(points))
    cells.append(row)

cells = th.list_to_tree(cells)