Assignment 3: Cluster Sprawls

Due: Friday, Feb 21, 2025

Important

Download the template Grasshopper document here: A3 Boilerplate.

Context

For this assignment, you’ll be writing code that interacts with PRNG functions from Python’s random module and with some grid-based geometry definitions to create interesting patterns.

In these patterns, you’ll have groups of points defined on a grid that are randomly connected into clusters of points. In the picture at the top of the page and right below, each cluster is colored differently.

In the Grasshopper definition, the points involved in the clusters are converted into circles that form the visual output. Creating these clusters starts with seeds, individual points chosen at random, from which the clusters will expand and “sprawl” until all points in the grid have been assigned to a cluster.

During each step of the sprawl, grid points on the frontier (those that are adjacent to points that have joined a cluster) are identified, and one frontier point is added to the smallest cluster it is adjacent to.

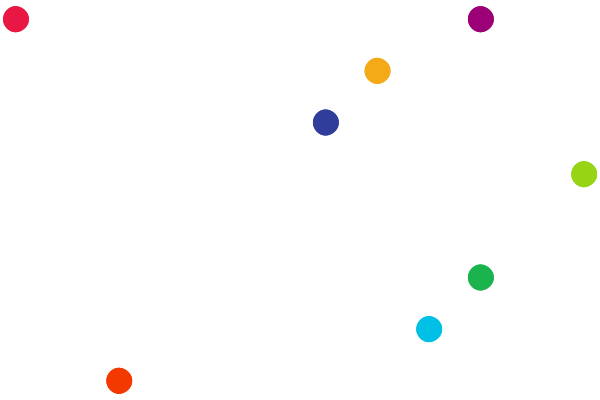
The seeds of the above example cluster sprawl.

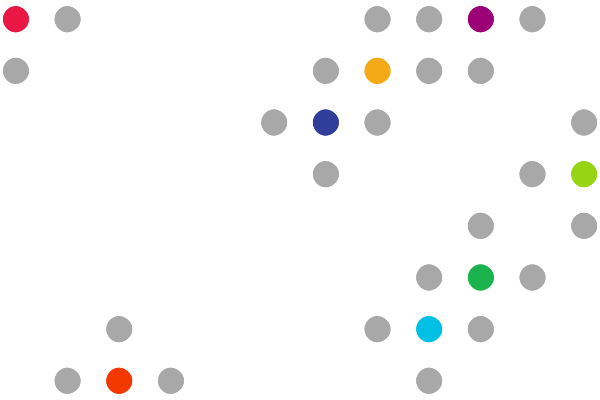
The frontier points at the first step of the sprawl are shown in grey.

In the picture showing the seeds with the initial frontier, notice how the seeds and frontier points are actually on a grid more sparse than the example crawl. This helps to facilitate a constant spacing between each cluster. In order to fill the gaps within a cluster, as points are added to the cluster, so is an edge. Internally, this is a 2-tuple: (start_point, end_point). When outputted, these edge points are placed as circles exactly halfway between start_point and end_point, forming the connections seen in the example. When a point is added to a cluster, one of the neighboring points in that cluster is selected for creating an edge between the added point and that selected point.

Additionally, points have a chance to form a second edge between an additional neighboring point in the cluster they’re being added to, creating additional visual interest.

Configuration

You have some options for configuring the output. In a group are a bunch of parameters that affect the generation:

Parameters Group

• Grid Height: The height of the grid.

• Grid Width: The width of the grid.

• Seed Count: The number of cluster seeds to create. This will also be the number of clusters in the final output.

• PRNG Seed: The seed provided to the pseudo-random number generator in the random module via random.seed().

• Two-Edges Chance: The probability that adding a point to a cluster will result in creating two edges, if possible.

Rendering Options Group

If you’d like, you can change some options used during rendering, like the origin of the grid, a uniform scaling factor, and a gradient that defines the colors used to differentiate groups.

Task Description

In the template Grasshopper file above, you will edit the Python 3 script node titled “Create Clusters”. The node itself will be red, and it’s contained in a group with the caption “Implement Me!”

Type Aliases

Near the top of the file, you’ll see a couple of type aliases that are used in type hints throughout the file. Using type aliases makes type-hinting functions and variables much easier. The following type aliases are defined for you:

• GridPoint: equivalent to tuple[int, int]

  • Points in the grid are identified by an (x, y) tuple, which are later converted to Vector3ds.

• ClusterEdge: equivalent to tuple[GridPoint, GridPoint]

  • Edges in a cluster are identified by a (start_point, end_point) tuple, which are later converted to Vector3ds as the midpoint between start_point and end_point.

• ClusterPoints: equivalent to dict[int, set[GridPoint]]

  • Clusters are stored in a map from the cluster number to the set of points contained in the cluster. Technically, this could be a list of sets of points, but I used a dictionary when I originally made the solution to this problem, so this is what you’ll get.

• ClusterEdges: equivalent to dict[int, list[ClusterEdge]]

  • Cluster edges are stored in a map from the cluster number to the list of edges created to connect the cluster points. Technically, this could also be a list instead of a dictionary.

Things to Implement

Inside the script, scroll down to the “Implementation” section. Here, you’ll be implementing two functions:

get_cluster_seeds(unclaimed: set[GridPoint]) → list[GridPoint]:

Sample cluster_seed_count GridPoints randomly from unclaimed, returning the sampled list.

select_point_to_add(frontier: list[GridPoint]) → GridPoint:

Select a random GridPoint from the frontier of unclaimed GridPoints adjacent to the current clusters.

create_clusters()

Additionally, you’ll see a function called create_clusters(). Inside of this, you’ll need to create the logic that connects a randomly-selected frontier point to a cluster, and you’ll need to do some bookkeeping.

At the first raise NotImplementedError in this function, you’ll need to create an edge or two:

1. Select a random point from the target_cluster_points to use as the edge endpoint.

2. Add the new ClusterEdge to cluster_edges[target_cluster] (this will be a 2-tuple with to_add and your selected endpoint).

3. Remove the selected endpoint from target_cluster_points.

4. If there are any remaining GridPoints in target_cluster_points:

   1. Sample a random number.

   2. If that random number is less than or equal to two_edges_chance:

      1. Pick a second random GridPoint from target_cluster_points.

      2. Create a new edge tuple with to_add and this second random GridPoint.

      3. Add this new edge to cluster_edges[target_cluster].

At the second raise NotImplementedError in create_clusters(), you’ll need to:

1. Add to_add to claimed, the set of claimed GridPoints.

2. Add to_add to the set of GridPoints at cluster_points[target_cluster].

3. Remove to_add from unclaimed.

Danger

If you do not correctly remove to_add from unclaimed, the while loop inside create_clusters() will loop forever, requiring you to force-crash Rhino. Do this first, or create some way to escape the loop, such as putting break somewhere inside the loop.

Tips

1. It’s very possible that you’ll make an endless loop for yourself if you don’t do the bookkeeping correctly. I’d suggest starting with that, and if you’re extra worried, you can also add an additional loop condition. Replace the while unclaimed: line with:

   loops = 0
   while loops < grid_height * grid_width and unclaimed:
       loops += 1
   

   This will break you out of the loop after enough iterations to guarantee that each point has been added to a cluster.

2. You can comment out the raise NotImplementedErrors in the loop where you’ll need to create edges, and you’ll be able to see if your implementations of get_cluster_seeds() and select_point_to_add() works as expected. I recommend changing the gradient to make the different clusters colored a little more obviously than the default green.

3. Take a look back at the Week 6 page on randomness for details on functions that you might find helpful during your implementation.

Submission

A Note on Randomness

This problem requires the use of the random module. This uses a pseudo-random number generator internally, which means any sequence of function calls is completely deterministic for a given seed. Importantly, if you use different functions from what I used, or if you use the same functions in a slightly different order, your solution will not produce exactly the same outputs as mine.

This is perfectly fine. I won’t be checking that your solution produces the exact same results as mine, but I will be checking that you actually do incorporate randomness from the random module.

Deliverables

When submitting your assignment, upload a .gh file containing your solution. Also create a handful (minimum 5) of pictures showcasing the rigorousness of your solution and its incorporation of randomness. This means you should play with different grid extents, seeds, two-edge chances, and seed counts. Feel free to also play with the colors used.

If you haven’t made renderings from Grasshopper, I’d suggest right-clicking the Custom Preview node, selecting Bake, changing your viewport to use the Rendered model view, and print out the surfaces you create to a picture.

Rubric

Points	Requirements
15	Your implementation for get_cluster_seeds() randomly samples GridPoints from unclaimed, returning a list of cluster_seed_count unique GridPoints.
15	Your implementation for select_point_to_add() randomly selects a GridPoint from frontier to return.
15	Your implementation of the edge creation process randomly selects a GridPoint from target_cluster_points and creates a ClusterEdge between it and to_add.
10	Your implementation of the edge creation process supports creating a second ClusterEdge between to_add and a random GridPoint from target_cluster_points, when a random roll is less than or equal to two_edges_chance.
5	Your implementation of the bookkeeping correctly performs all 3 required actions.
40	You have created at least 5 pictures showcasing the rigorousness of your solution.